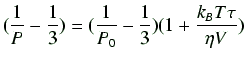: 問題2
: 問題
: 問題
図 21:
DNSという色素でラベルした免疫グロブリンの蛍光偏光度。
温度と水溶液中のsucrose(砂糖)濃度を変えて、溶液の粘性を変化させて測定したもの。左図は、
同じsucrose濃度について、右図は、同じ温度について直線を引いた。
|
|
図21はDNS色素でラベルした免疫グロブリンというタンパク
質の蛍光偏光度(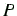 )を測定したデータである。溶液中にサッカロースを加
えて粘性を変えて、さらに種々の温度で測定したデータを、左図は同じサッカ
ロース濃度について直線を引き、右図は同じ温度について直線を引いたもので
ある。蛍光偏光度
)を測定したデータである。溶液中にサッカロースを加
えて粘性を変えて、さらに種々の温度で測定したデータを、左図は同じサッカ
ロース濃度について直線を引き、右図は同じ温度について直線を引いたもので
ある。蛍光偏光度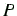 とは、慣用的に用いられるパラメーターで、入射偏光に
平行と垂直のふたつの偏光蛍光成分
とは、慣用的に用いられるパラメーターで、入射偏光に
平行と垂直のふたつの偏光蛍光成分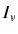 と
と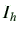 を用いて、
を用いて、
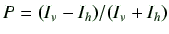 |
(43) |
と定義される。テキストで記述している蛍光異方性rとは、
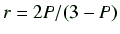 |
(44) |
と関係づけられる。この蛍光偏光度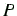 を用いると、テキスト本文11式の
ペラン・ウェーバーのプロットは、
を用いると、テキスト本文11式の
ペラン・ウェーバーのプロットは、
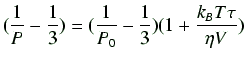 |
(45) |
と書くことができる。図21の右図から、
| ℃ |
切片(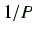 ) ) |
傾き(
 )) )) |
| 10 |
2.51 |
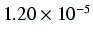 |
| 20 |
2.59 |
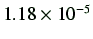 |
| 35 |
2.73 |
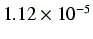 |
| 45 |
2.85 |
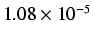 |
となる。ここで、切片とは
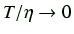 の
の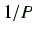 の値、傾きとは
の値、傾きとは に対する
に対する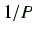 の変
化量である。この値と緩和時間
の変
化量である。この値と緩和時間
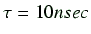 を用いて、各温度における免疫グロ
ブリンの回転体積
を用いて、各温度における免疫グロ
ブリンの回転体積 を算出せよ。回転体積の温度依存性について、考えられる
原因をあげよ。また、免疫グロブリンの分子量150000と比重
を算出せよ。回転体積の温度依存性について、考えられる
原因をあげよ。また、免疫グロブリンの分子量150000と比重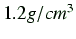 を仮定し
て、免疫グロブリン1分子が占める空間的な体積を算出し、回転体積と比較せ
よ。(計算の際、数値だけを計算するようなことをせず、必ず単位も式の中に
入れて計算すること。これにより、
を仮定し
て、免疫グロブリン1分子が占める空間的な体積を算出し、回転体積と比較せ
よ。(計算の際、数値だけを計算するようなことをせず、必ず単位も式の中に
入れて計算すること。これにより、 が体積の次元になっていることを確認せ
よ。)
が体積の次元になっていることを確認せ
よ。)
![\includegraphics[width=10cm,clip]{problem1.eps}](img150.png)
![\includegraphics[width=10cm,clip]{problem1.eps}](img150.png)
![]() )を測定したデータである。溶液中にサッカロースを加
えて粘性を変えて、さらに種々の温度で測定したデータを、左図は同じサッカ
ロース濃度について直線を引き、右図は同じ温度について直線を引いたもので
ある。蛍光偏光度
)を測定したデータである。溶液中にサッカロースを加
えて粘性を変えて、さらに種々の温度で測定したデータを、左図は同じサッカ
ロース濃度について直線を引き、右図は同じ温度について直線を引いたもので
ある。蛍光偏光度![]() とは、慣用的に用いられるパラメーターで、入射偏光に
平行と垂直のふたつの偏光蛍光成分
とは、慣用的に用いられるパラメーターで、入射偏光に
平行と垂直のふたつの偏光蛍光成分![]() と
と![]() を用いて、
を用いて、