... かれている。Ｃ言語の入門書は書店に行けば数多くあるが1
参考図書 (1) はかなりお勧めである。 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... さて、プログラムを見てみよう。2
このプログラム名についている ``ludolph'' はドイツで使われている円周率の別称、ルドルフ数(die Ludolphsche Zahl)からきている。ドイツの数学者 Ludolph Van Ceulen(1540− 1610) は生涯をかけて円周率の計算した。その精度は小数点以下 35 桁 (3.14159265358979323846264338327950288)である。 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... この2行で疑似乱数を生成する。乱数発生法はここでは省略する3
この 方法は線形合同法と呼ばれる。適当な (IA,IC,IM) の組を用いて、 (iseed*IA+IC) を IM で割った時の余りを求める。この余りを IM で割れば 0 から 1 までの任意の数になり、更にこの余りを iseedに代入して、再び同じ計算を繰り返していくことで、0 から 1 ま での「ある一定周期内での」ランダムな数列を作ることができる。この周期は (IA,IC,IM) の組合せによって決まる。参考図書(2) 第 7 章にその具 体的な数値が 示してある。 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 用例を示す。4
Mac ユーザなら一目瞭然かも知れない 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... の様に進むことにする5
このルールは(1 次元の問題を除けば)一番簡単 なルールである。例えば 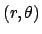$(r,\theta)$ を乱数で振るようにすれば、ブラウン運 動のシミュレートなども可能である(参考図書 (5))。 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.